今回の話はカラパイアという情報サイトに掲載された記事がきっかけ、
●タイムトラベルの実現に近づいたのか?ブラックホールを利用したワープ航法で光速より速く移動できる(米研究)
2019/1/22 カラパイヤより
まず目に飛び込んだのは「光速より速く移動できる」という言葉、さらに「タイムトラベル」や「ワープ航法」などの魅惑的なキーワードが並んでいる。
だがこの宇宙では通常の物質は光速度を超えることはできない。
例えば「文系でもわかるホーキング博士の最後の論文解説(2)」でもご紹介している通り、物質が光の速度に近づいていくとローレンツ収縮により長さがどんどん短くなってしまう。
だから「ついに光速度を超える方法を発見したのか!」と勢い込んで記事を読んだところ、紹介されていたのは「回転するブラックホールに関する新しい研究成果」で、残念ながら「光より速く進める具体的な方法」ではなかった。
なぜこんなキーワードが並んだのか気になってカラパイヤの参考記事をたどったところ、ある論文に行き着いた。
●急速に回転するカー・ブラックホールのコーシー地平線に接近する物理的物体
2018/7/17初稿 2018年12月6日更新 arXivより
この論文は米マサチューセッツ大学のキャロライン・マラリー博士とガウラフ・カンナ博士、そしてジョージア・グウィネット大学のリオール・M・ブルコー博士らの研究成果である。
論文の内容がかなり難しく私には詳細な把握ができなかったので、執筆者の一人ガウラフ・カンナ博士の海外科学雑誌のインタビュー、
●おそらくあなたはブラックホールを使って宇宙を旅することができる
2019/1/25 Discoverより
を参考にしながら、回転するブラックホールの概要を加え、「光速度を超える方法」や「タイムトラベル」、「ワープ航法」というキーワードがこの論文からどのように導かれたのかをご紹介したい。
まずブラックホールの基本的な知識だが、太陽の30倍以上もある星が死を迎えると自身の質量を支えることができずどんどん小さくつぶれていき、ついには強大な重力をもったブラックホールとなる。
ブラックホールの中心には密度無限の「特異点」があるとされ、その周囲は強い重力によって時空がゆがめられ、中心からある距離以内に入ると脱出速度が光速を超えて光でさえも抜け出すことのできない「事象の地平面」に囲まれている。
この一度入ると脱出不可能な距離を「シュヴァルツシルト半径」と呼び、ドイツの天文学者カール・シュヴァルツシルトがアインシュタイン方程式から導き出した。
中心に特異点をもち、周囲を事象の地平面に囲まれた一番ポピュラーなブラックホールを「シュヴァルツシルト・ブラックホール」と呼ぶ。
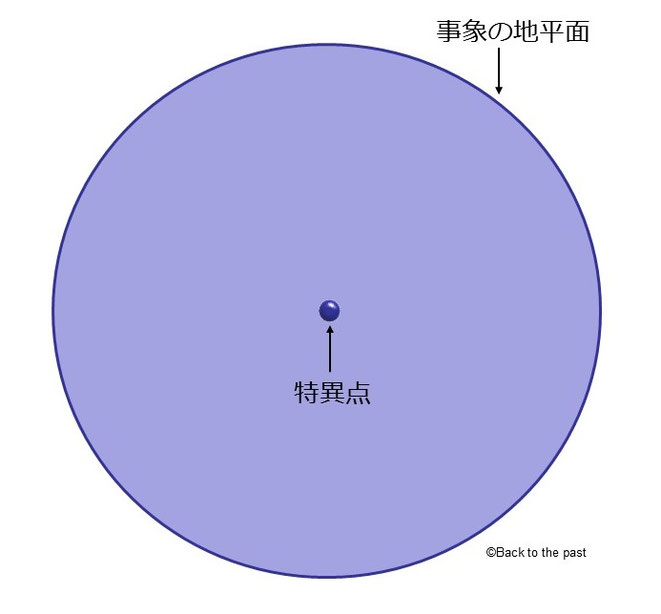
シュバルツシルト・ブラックホール
今回カンナ博士らが注目したのはシュヴァルツシルト・ブラックホールとは違う、「回転しているブラックホール」だ。
この回転するブラックホールは1963年にその理論を発表したニュージーランドの数学者ロイ・カーの名前にちなんで「カー・ブラックホール」と呼ばれる。
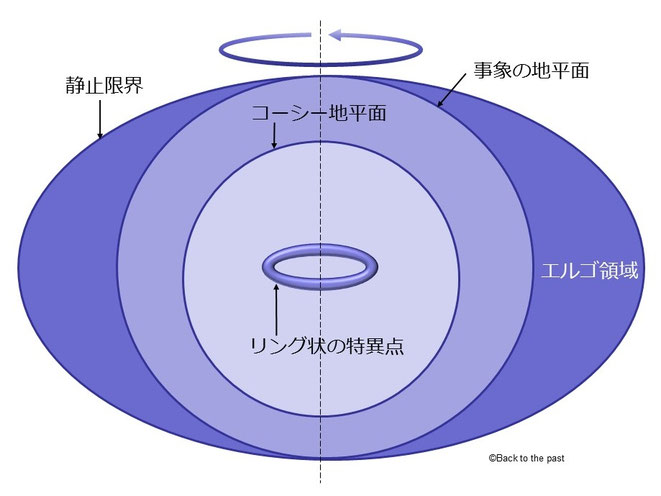
カー・ブラックホール
カー・ブラックホールは回転しているので、強い重力でゆがめられた周囲の時空が引きずられて渦を巻いている。
例えば宇宙船がカー・ブラックホールに近づいていくと、ブラックホールの中心に向かって引っぱられるとともに、この渦によって横方向からも力を受ける。
横方向からの力によって宇宙船はカー・ブラックホールの周囲を回転するので、同じ位置に留まりたいのなら回転と逆方向にロケットを噴射し続けなければならない。
さらに宇宙船がブラックホールに近づくと、どんなにロケットを噴射しても、渦の勢いが強すぎて同じ場所に留まれなくなる限界に達する。これを「静止限界」と呼ぶ。
静止限界を超えると渦に押し流されて、宇宙船はカー・ブラックホールの周囲を回転するが、事象の地平面より手前なので、まだかろうじてブラックホールから脱出することができる。事象の地平面と静止限界に囲まれた範囲を「エルゴ領域」と呼ぶ。
宇宙船がエルゴ領域を進んでいくとやがて事象の地平面に到達する。カー・ブラックホールには事象の地平面の内側にさらにもう1つ「コーシー地平面」が存在する。
このコーシー地平面の内側には特異点があるが、カー・ブラックホールは回転しているので特異点が遠心力のためにリング状に広がっている。
シュヴァルツシルト・ブラックホールに入った宇宙船は無限の密度が1点に集中した特異点にぶつかって破壊されてしまう。
しかしカー・ブラックホールならば、宇宙船が特異点のリングを避けてその中心に突入できれば、無事通過できるのではないかと考えられていた。
カンナ博士らがこの論文を書いた動機は、ノーベル賞受賞者のキップ・ソーン博士が監修したSF映画「インターステラー(字幕版)」に登場する「ガルガンチュア」という名の巨大な回転するカー・ブラックホールに実際に宇宙船が入ったらどうなるのか確かめたかったからだ。実際にその様子をスーパーコンピュータでシミュレーションした。
すると驚いたことに大質量の回転するブラックホールの特異点は非常に穏やかで「弱く」、宇宙船が安全に通過できることがわかった。
カンナ博士はこの理由を、熱く燃えさかる2000度のろうそくでも、すばやく指を通過させれば火傷しないのに似ていると説明する。
さらに事象の地平面を超えた宇宙船はスパゲッティのように激しく伸縮されると考えられているが、インターステラーに登場するガルガンチュアのような巨大なサイズのカー・ブラックホールの場合、その影響はかなり小さいことがわかった。
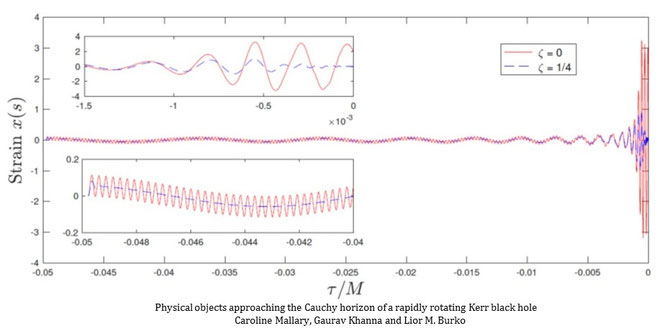
カー・ブラックホールに侵入した宇宙船が受ける物理的なひずみ(カンナ博士らの論文より)
※このグラフはカー・ブラックホールに侵入した宇宙船のボディが受ける物理的なひずみを表している(縦軸がひずみ、横軸が時間の経過)。
青色が「減衰あり」の場合で赤色が「減衰なし」の場合。重要なのはどちらのひずみもブラックホール近くで劇的に増加するが、その影響は有限で、効果が永遠には増大しない点だ。
カンナ博士によれば今回のシミュレーションは周囲の星や放射線などのかく乱の影響を考慮していない孤立化したモデルなので、星や塵やガスや放射線に囲まれた現実のブラックホールにそのまま適用することはできない。
しかし今回の研究により、巨大なカー・ブラックホールならば、宇宙船がコーシー地平面を超えて無事にリング特異点を通過できる可能性が示された。
特異点は無限の密度によって時空そのものに穴が開いており、その穴を入り口にして無事通過することができれば別の宇宙、別の時間へ旅することができるかもしれない。
時空をショートカットして短期間で宇宙規模の長距離移動ができれば「ワープ航法」であり、光の速度を越えて移動できるとも言える。
距離ではなく時間を飛び越えれば「タイムトラベル」になる。
カラパイヤのSF的なキーワードはこのあたりから導き出されたようだ。
今回の論文で利用された巨大なカー・ブラックホールは実はわれわれが住む天の川銀河の中心にも存在する可能性がある。
※例えば27,000光年先にある「いて座A*」。
あながち夢物語ではないのだ。
この論文は「タイムマシンの物理学」にとって重要な研究の1つになるだろう。









